Imagine you have a little trolley with a maximum load of 200Kg (20000 gram), and you get one chance to transport rocks of different weights, each has a reward value from location A to location B, and you are not allowed to load more than 200Kg of rocks. You want to pick the most possible weight for the highest possible reward.
What would you do to calculate your reward?
You can of course count it manually and it will take a lot of time for a little list of raw items, but if the list becomes big enough that it will take you long time to calculate. Then KnapSack Algorithm is your best friend.
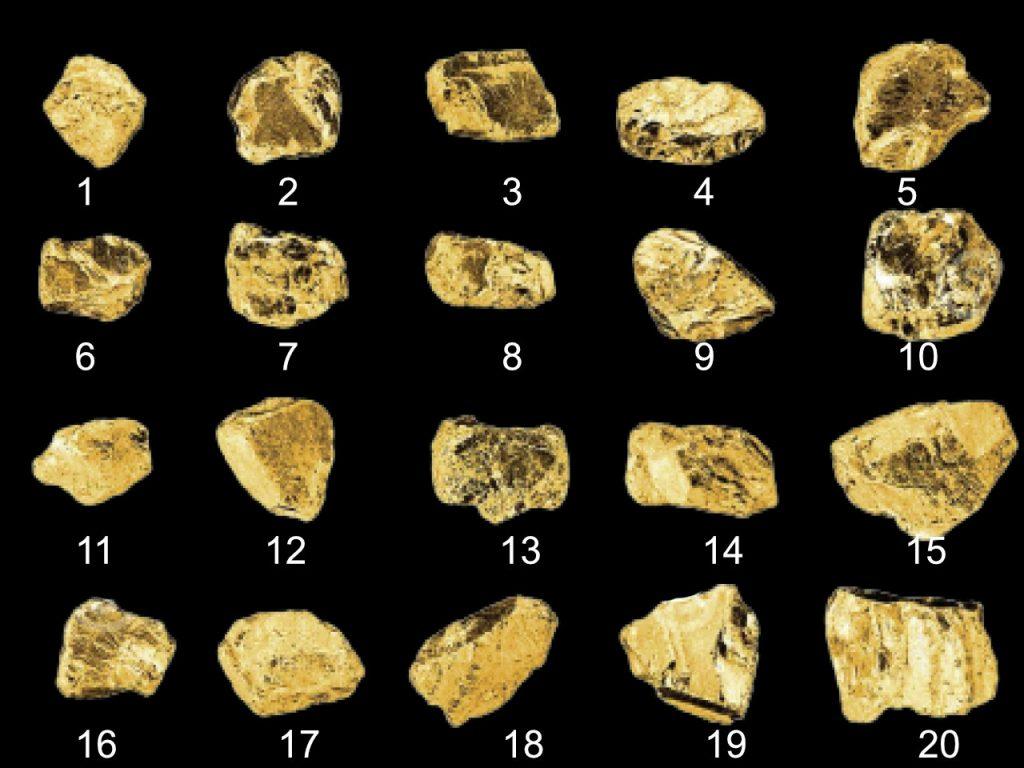
Here is a specific example, as you can see the in image above, we have gold rocks labled from 1 to 20. The size of rock does not mean more reward, it is all about the weight of the rock and how much gold value it contains.
Her is the list:
| Rock number | Weight in Gram | Reward |
| 1 | 5724 | 17,74 |
| 2 | 9873 | 37,12 |
| 3 | 13492 | 46,14 |
| 4 | 7727 | 30,44 |
| 5 | 2924 | 10,64 |
| 6 | 1544 | 5,00 |
| 7 | 7082 | 28,18 |
| 8 | 13960 | 50,82 |
| 9 | 6371 | 22,94 |
| 10 | 14380 | 53,20 |
| 11 | 19045 | 58,66 |
| 12 | 14057 | 13,72 |
| 13 | 7082 | 28,18 |
| 14 | 13960 | 50,82 |
| 15 | 6371 | 22,94 |
| 16 | 13380 | 53,20 |
| 17 | 19045 | 58,66 |
| 18 | 7057 | 12,72 |
| 19 | 19045 | 58,66 |
| 20 | 6057 | 3,72 |
KnapSack algorithm can help solve this problem. So in this article, I will implement a recursive version of knapsack using C#. The implementation is simple and straightforward. In my case, I will use a knapsack to calculate my highest possible reward for maximum possible weight, but this does not mean which rock is less worth taking. In my approach, I will sub up the rock and subtract the results from the knapsack, that way I will find out which rock should be left behind.
Let’s do it.
I will create a class called it Knapsack.
It has a method that takes our rock data and the maximum allowed weight. My Data class contain a list of rock weights in gram and a reward for each rock, as you saw earlier in the rock list.
public class KnapSack
{
public decimal Calculate(IReadOnlyList<Data> data, int maxWeight)
{
var bonus = data.Select(e => e.Value).ToArray();
var weights = data.Select(e => (double)e.Weight).ToArray();
return (decimal)Calculate(maxWeight, weights, bonus, bonus.Length);
}
private static double Calculate(double weight, IReadOnlyList<double> weights, IReadOnlyList<double> values, int n)
{
var idx = n - 1;
if (n <= 0 || weight <= 0.0) return 0;
if (weights[idx] > weight)
{
return 0;
}
var a = values[idx] + Calculate(weight - weights[idx], weights, values, idx);
var b = Calculate(weight, weights, values, idx);
var result = Max(a, b);
return result;
}
private static double Max(double a, double b)
{
return a > b ? a : b;
}
}My data class model has dummy data as shown in the rock list.
public class Data
{
public int Id { get; set; }
public string Description { get; set; }
public int Weight { get; set; }
public double Value { get; set; }
public Data(int id, string description, int weight, double value)
{
Id = id;
Description = description;
Value = value;
Weight = weight;
}
public static List<Data> RawMaterials()
{
return new List<Data>
{
new Data(1, "Rock1", 5724, 17.74),
new Data(2, "Rock2,9873, 37.12),
new Data(3, "Rock3",13492, 46.14),
new Data(4, "Rock4",7727, 30.44),
new Data(5, "Rock5",2924, 10.64),
new Data(6, "Rock6",1544, 5),
new Data(7, "Rock7",7082, 28.18),
new Data(8, "Rock8",13960, 50.82),
new Data(9, "Rock9",6371, 22.94),
new Data(10, "Rock10",14380, 53.2),
new Data(11, "Rock11",19045, 58.66),
new Data(12, "Rock12",14057, 13.72),
new Data(13, "Rock13",7082, 28.18),
new Data(14, "Rock14",13960, 50.82),
new Data(15, "Rock15",6371, 22.94),
new Data(16, "Rock16",13380, 53.2),
new Data(17, "Rock17",19045, 58.66),
new Data(18, "Rock18",7057, 12.72),
new Data(19, "Rock19",19045, 58.66),
new Data(20, "Rock20",6057, 3.72)
};
}
}I will also create a config class
public static class Config
{
public const int MaxWeight = 200000;
}Finally, let’s run our knapsack in the main method.
public static void Main(string[] args)
{
var calculator = new KnapSack();
var result = calculator.Calculate(Data.RawMaterials(), Config.MaxWeight);
Console.WriteLine($"Max bonus for {Config.MaxWeight} weight is: {result} money unit");
var sum = (decimal)Data.RawMaterials().Sum(e => e.Value);
var exclude = sum - result;
Console.WriteLine($"Which rock value to exclude {exclude}");
}When we run this method, we will get this output:
Max bonus for 200000 weight is: 649,78 money unit
Which rock value to exclude 13,72
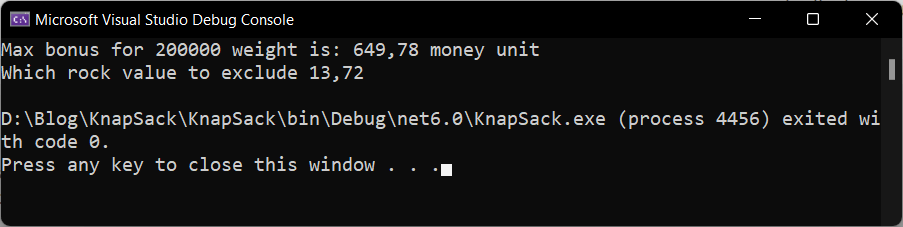
When we check the rock with a value of 13,72, we will find out it is rock 12 that we should exclude from the transport. That said this is only an example of a knapsack, if you exclude multiple items, you may need to implement the dynamic version of the knapsack.
So now let’s sum up all rock’s weight without rock 12, we will get 194119 gram which is the maximum weight we can take with us for the highest reward.
Conclusion
As you can see, with few lines of code, knapsack algorithms are able to calculate very complex problems and complicated problems. As mentioned our algorithm is recursive, which means it does have an efficient running time. In this example we are lucky that only one element was removed (rock 12) and it was easy to predict, but how about removal of multiple items? This is what I will cover in Part 2 of this article where I will improve running time using a dynamic programming approach and that will help me keep track on index of removed or included items. Maybe I have been very optimistic using the gold rocks as an example, but the same type of algorithm can be used for calculating crypto mining block rewards or other application types. If you take the rock list and calculate it in excel ark, you will end up excluding rock number 12. Give it a try😜

