As we talked about in the last article, we used the recursive approach of KnapSack and we have had 2 drawbacks. It is heavy in running time and it is not possible to track the index of removed items. In this part, we will take the Dynamic part approach which will improve running time and help us track the item’s index.
Let’s use the same image example and the example of a list of rocks from the last article.
Her is the list:
| Rock number | Weight in Gram | Reward |
| 1 | 5724 | 17,74 |
| 2 | 9873 | 37,12 |
| 3 | 13492 | 46,14 |
| 4 | 7727 | 30,44 |
| 5 | 2924 | 10,64 |
| 6 | 1544 | 5,00 |
| 7 | 7082 | 28,18 |
| 8 | 13960 | 50,82 |
| 9 | 6371 | 22,94 |
| 10 | 14380 | 53,20 |
| 11 | 19045 | 58,66 |
| 12 | 14057 | 13,72 |
| 13 | 7082 | 28,18 |
| 14 | 13960 | 50,82 |
| 15 | 6371 | 22,94 |
| 16 | 13380 | 53,20 |
| 17 | 19045 | 58,66 |
| 18 | 7057 | 12,72 |
| 19 | 19045 | 58,66 |
| 20 | 6057 | 3,72 |
Let’s do it.
Dynamic Programming in general builds a matrix for memorization of the calculation steps. Let’s start with illustrating the matrix of calculation.
I will create a class called it KnapsackDp. It has some similarities to our Knapsack class from the last article, with some changes.
It has a constructor that takes our rock data and the maximum allowed weight. My Data class contain a list of rock weights in gram and a reward for each rock, as you saw earlier in the rock list.
public class KnapSackDp
{
private readonly IReadOnlyList<Data> _data;
private readonly Result _result;
public KnapSackDp(IReadOnlyList<Data> data, int maxWeight)
{
var bonus = data.Select(e => e.Value).ToArray();
var weights = data.Select(e => e.Weight).ToArray();
_data = data;
_result = Calculate(maxWeight, weights, bonus, bonus.Length);
}
public Result Calculate()
{
return _result;
}
private Result Calculate(int weight, IReadOnlyList<int> weights, IReadOnlyList<double> values, int n)
{
int i;
int w;
double[,] matrix = new double[n + 1, weight + 1];
for (i = 0; i <= n; i++)
{
for (w = 0; w <= weight; w++)
{
var idx = i - 1;
if (i == 0 || w == 0)
{
matrix[i, w] = 0;
}
else if (weights[idx] <= w)
{
var a = values[idx] + matrix[idx, w - weights[idx]];
var b = matrix[idx, w];
matrix[i, w] = Max(a, b);
}
else
{
matrix[i, w] = matrix[idx, w];
}
}
}
var result = new Result();
double value = matrix[n, weight];
result.Value = value;
result.Weights = new List<Data>();
w = weight;
for (i = n; i > 0 && value > 0; i--)
{
if (w < 0 || Math.Abs(value - matrix[i - 1, w]) == 0)
{
continue;
}
var data = result.GetData(_data.ToList(), i);
if (data != null)
{
result.Weights.Add(data);
}
value -= values[i - 1];
w -= weights[i - 1];
}
return result;
}
private static double Max(double a, double b)
{
return a > b ? a : b;
}
}My data and result class model has dummy data as shown in the rock list.
public class Data
{
public int Id { get; set; }
public string Description { get; set; }
public int Weight { get; set; }
public double Value { get; set; }
public Data(int id, string description, int weight, double value)
{
Id = id;
Description = description;
Value = value;
Weight = weight;
}
public static List<Data> RawMaterials()
{
return new List<Data>
{
new Data(1, "Rock1", 5724, 17.74),
new Data(2, "Rock2,9873, 37.12),
new Data(3, "Rock3",13492, 46.14),
new Data(4, "Rock4",7727, 30.44),
new Data(5, "Rock5",2924, 10.64),
new Data(6, "Rock6",1544, 5),
new Data(7, "Rock7",7082, 28.18),
new Data(8, "Rock8",13960, 50.82),
new Data(9, "Rock9",6371, 22.94),
new Data(10, "Rock10",14380, 53.2),
new Data(11, "Rock11",19045, 58.66),
new Data(12, "Rock12",14057, 13.72),
new Data(13, "Rock13",7082, 28.18),
new Data(14, "Rock14",13960, 50.82),
new Data(15, "Rock15",6371, 22.94),
new Data(16, "Rock16",13380, 53.2),
new Data(17, "Rock17",19045, 58.66),
new Data(18, "Rock18",7057, 12.72),
new Data(19, "Rock19",19045, 58.66),
new Data(20, "Rock20",6057, 3.72)
};
}
}
public class Result
{
public List<Data>? Weights { get; set; }
public IOrderedEnumerable<Data>? Ordered => Weights?.OrderBy(e => e.Id);
public double Value { get; set; }
public Data? GetData(List<Data> data, int idx)
{
return data.Find(e => e.Id == idx);
}
}I will also create a config class
public static class Config
{
public const int MaxWeight = 200000;
}Finally, let’s run our knapsack in the main method.
public static void Main()
{
var ks = new KnapSackDp(Config.RockData(), Config.MaxWeight);
var calculate = ks.Calculate();
if (calculate.Ordered == null) return;
foreach (var data in calculate.Ordered)
{
Console.WriteLine(data.ToString());
}
if (calculate.Weights != null)
{
var sum = $"{calculate.Weights.Sum(e => e.Value),34:F}";
Console.WriteLine(sum);
}
Console.WriteLine();
var result = $"{calculate.Value,34:F}";
Console.WriteLine(result);
}When we run this method, we will get this output:
1 Rock1 5724 17,74
2 Rock2 9873 37,12
3 Rock3 13492 46,14
4 Rock4 7727 30,44
5 Rock5 2924 10,64
6 Rock6 1544 5,00
7 Rock7 7082 28,18
8 Rock8 13960 50,82
9 Rock9 6371 22,94
10 Rock10 14380 53,20
11 Rock11 19045 58,66
13 Rock13 7082 28,18
14 Rock14 13960 50,82
15 Rock15 6371 22,94
16 Rock16 13380 53,20
17 Rock17 19045 58,66
18 Rock18 7057 12,72
19 Rock19 19045 58,66
20 Rock20 6057 3,72
649,78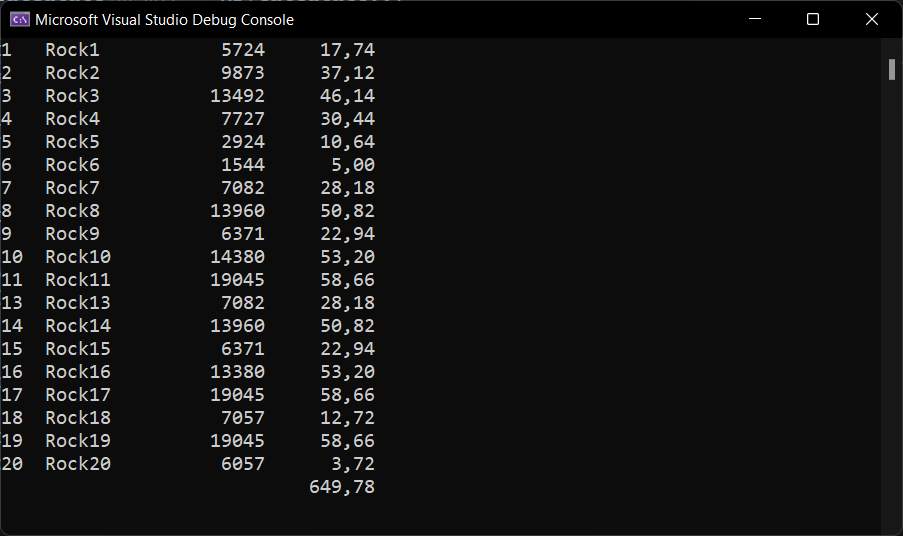
As we can see, all items are included, except item 12. This is exactly what we calculated in last article. But here we have a list of item we need to pick up in our trolley.
Conclusion
As you can see, with few lines of code, knapsack algorithms are able to calculate very complex problems and complicated problems. With this approach, we get better performance and index of included items. I am pretty sure this Algorithm has a place for more performance and clean up. But this is not the intention of this article. Enjoy.

