Evaluation
Evaluation is important and a key process in a project completion. This evaluation is to present the results of our system, for locating the trackable object position and track its (movement) repositioning over time using mobile smartphones as data collectors. The usability of the system relies on the results collected from mobile smartphone over time, more collection from more users means better results and improving of accuracy. Accuracy in this context means predicting the position of the mobile smartphone in testbed 4.1 (PitLAB) as good as possible at each direction as demonstrate in this picture 4.8. Hence this is an experimental use case, the testbed (PitLAB) environment we use does include everything from people sitting around, obstacles and furniture’s etc. as shown in panoramic image 4.2.
Note: The pictures might have changed during the project period, since the PitLAB was under construction during this study.
 Figure 4.1: Testbed at PitLAB, the yellow circles indicate three trackable objects. In this picture we want to demonstrate how things look in PitLAB and some of the trackable object’s true positions. In our experiment we use only one trackable object.
Figure 4.1: Testbed at PitLAB, the yellow circles indicate three trackable objects. In this picture we want to demonstrate how things look in PitLAB and some of the trackable object’s true positions. In our experiment we use only one trackable object.
4.1 Experimental Setup
The setup of the system, means having 14 iBeacons mounted with fixed positions of X and Y axis (all distances are demonstrated in figure 4.4) in relatively equal distance distribution of each axis. The height of the iBeacons from the floor is around
2100-2300mm this is hence to room structure and furniture 4.2.
The idea is that the user has a smartphone with our Mobile Client application running on it. The user lets the smartphone collects data form the surrounding iBeacons like the RSSI-values and UUID/MAC address. The system then uses RSSI data to predict the position of the smartphone in the room.
 Figure 4.2: PitLAB Panoramic view, a scale image version of this is in appendix chapter. If we zoom in the image we can see the nature of PitLAB. People, furniture in different heights, work-space and desks etc.
Figure 4.2: PitLAB Panoramic view, a scale image version of this is in appendix chapter. If we zoom in the image we can see the nature of PitLAB. People, furniture in different heights, work-space and desks etc.
4.1.1 Trackable object
We use the same iBeacon type for our trackable object, the only different is our trackable object does not have a fixed position. The height of the iBeacon is 1200mm mounted on an retried flag pole 4.3.
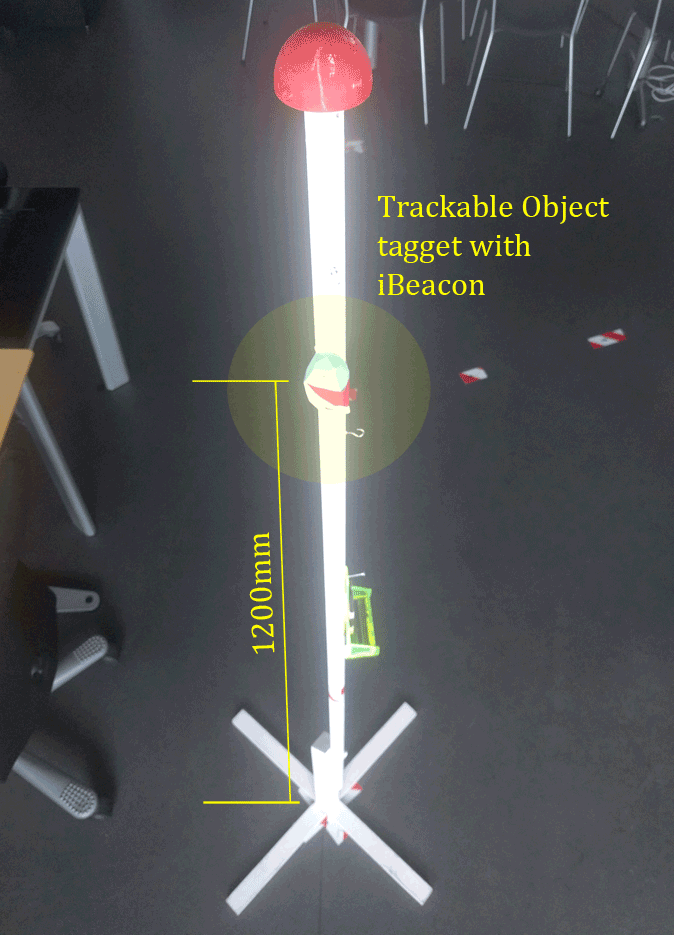 Figure 4.3: Trackable object (Pole) tag with iBeacon. We asked the Facility Management department of the IT-University if they could provide a pole for testing, and luckily they had some old flag poles which have been used throughout the study.
Figure 4.3: Trackable object (Pole) tag with iBeacon. We asked the Facility Management department of the IT-University if they could provide a pole for testing, and luckily they had some old flag poles which have been used throughout the study.
 Figure 4.4: iBeacon fixed position in room. Here we show the PitLAB room top view and how 14 iBeacons with fixed positions are placed in the room
Figure 4.4: iBeacon fixed position in room. Here we show the PitLAB room top view and how 14 iBeacons with fixed positions are placed in the room
4.1.2 iBeacon specification
All our iBeacons are Estimote 4.5 brand. The two most important configuration of iBeacons is transmitting power (TxPower) and advertising period. TxPower is set to
-12dB and advertising is set to 967ms on all iBeacons.
Figure 4.5: Estimote iBeacons
4.1.3 Smartphone
The smartphone is from Google, model LG Nexus 5x. Regarding to recent research made by Fürst [7], the IT-University, this smartphone should be the best phone to receive iBeacon signals. It makes it a suitable choice for our project.
4.2 Experiment
We mark the floor with four positions, called true positions: A, B, C and D. At each true position we have four directions: 0, 90, 180 and 270 degrees, 0 is almost on Earth North direction, as demonstrated in picture 4.8.
We collect data from all iBeacons (fixed position iBeacons and trackable object iBeacon) from each direction over 60 seconds of time. We hold the smartphone in our hand, centered to the body front as demonstrated in the picture 4.8. We repeat this in four rounds.
For instance if the trackable object is placed on C, we collect data from true position A Round 1 and true position B Round 2 from all directions. We continue to move the trackable object to D, and collect from true position B Round 1 and true position C Round 2 until trackable object has been through all true positions as shown in the experiment table 4.7.
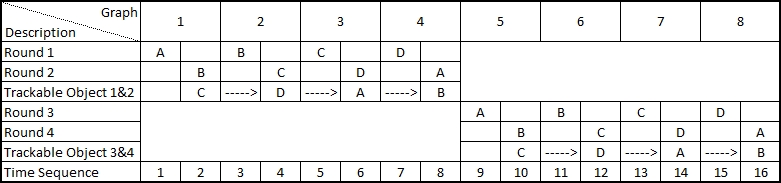 Figure 4.7: This table presents rounds and the time sequence. Round 1 and Round 2 are parallel rounds, but if we predict smartphone at A and predict smartphone at B, we predict trackable object at C. Later in this section eight different graphs will be presented (Graph1 to Graph8). These represent the results of the experiments.
Figure 4.7: This table presents rounds and the time sequence. Round 1 and Round 2 are parallel rounds, but if we predict smartphone at A and predict smartphone at B, we predict trackable object at C. Later in this section eight different graphs will be presented (Graph1 to Graph8). These represent the results of the experiments.
 Figure 4.8: A person holding smartphone testing RSSI receiving signals at Round 3 in true position B on angle 180° direction.
Figure 4.8: A person holding smartphone testing RSSI receiving signals at Round 3 in true position B on angle 180° direction.
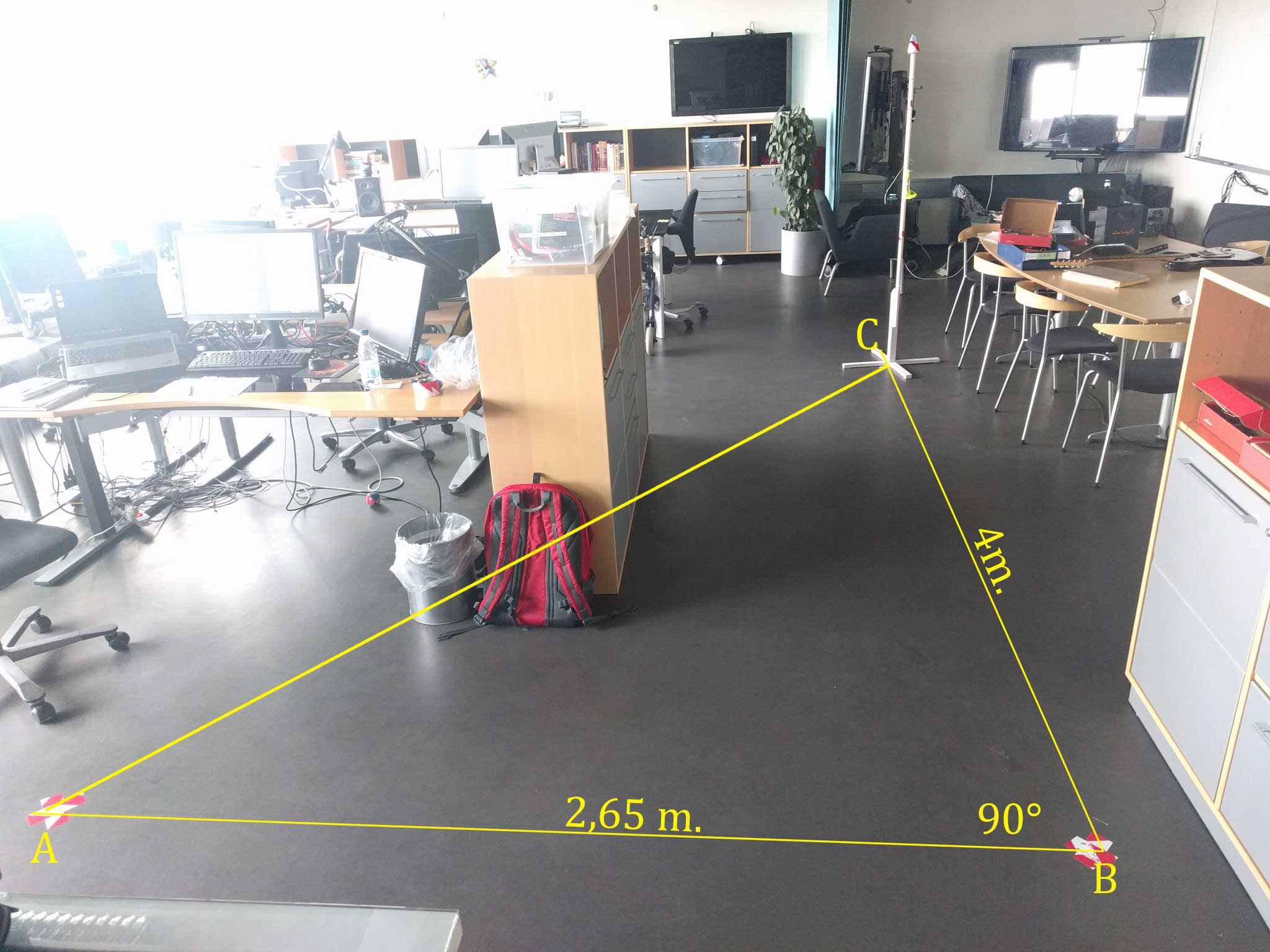 Figure 4.9: Testbed at PitLAB. We show here for instance Round 3, where the user test smartphone at true position A and move to true position B to predict trackable object at true position C
Figure 4.9: Testbed at PitLAB. We show here for instance Round 3, where the user test smartphone at true position A and move to true position B to predict trackable object at true position C
4.3 Results and analysis
In experiments from Round 1 and Round 2, we have totally 19 trackable objects estimation results and Round 3 and Round 4 from 23 trackable object estimation results. The Red mark belongs to true position C, Green belongs to true position D, Blue belongs to true position A and Orange belongs to true position B. For each colour cluster, we calculate a centroid of the collect data and represent this in bigger circle. We have added a horizontal and vertical line in centre of our graph in which each true position gets its own region respectively region AR, BR, CR and DR. The cross (+ sign) in graph represent the true position of the trackable object as demonstrate in graph 4.10 and graph 4.11.
As it appears for Round 1 and 2, the position of Red centroid belongs to CR region, Green belong to DR, Blue belongs to AR, expect the last one Orange which belongs to AR. However, Round 3 and 4, all colour belong to their respective regions (we calculate our centroid by taking the average of x and y for each cluster).
Graph 1 4.10 shows the result from Round 1 and 2 and Graph 2 4.11 show the result of round 3 and 4.
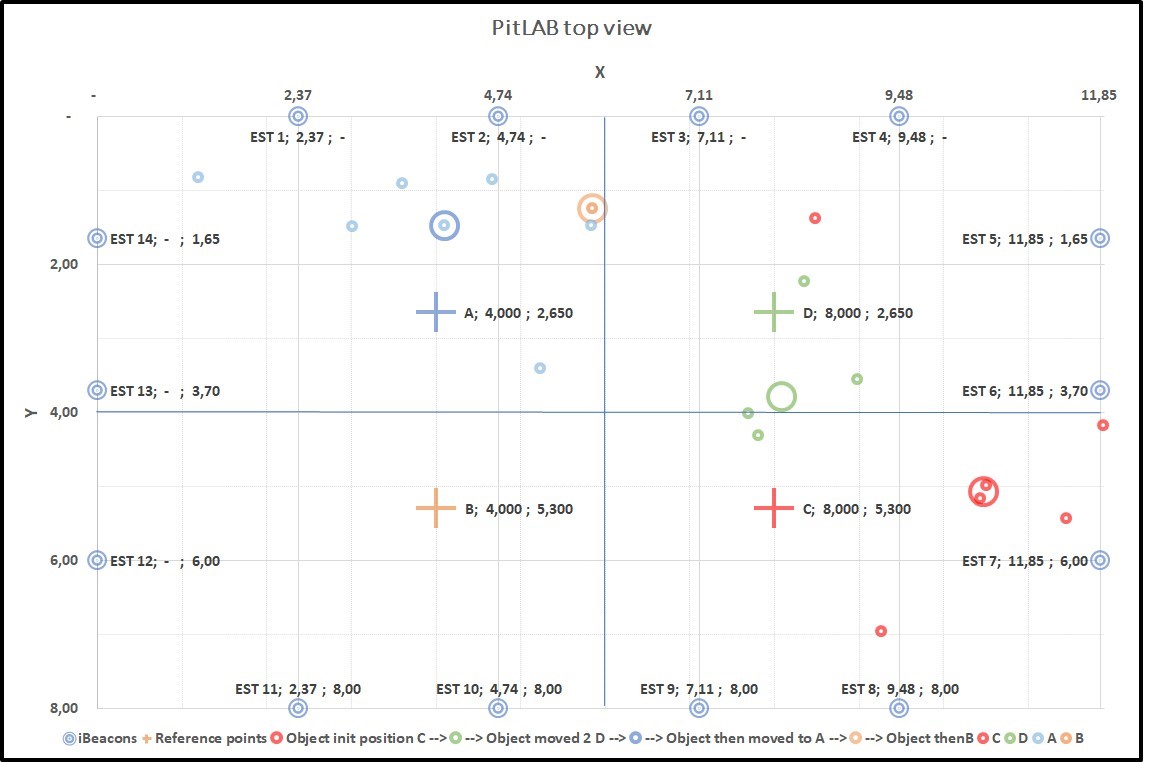 Figure 4.10: Round 1 and 2, (+) sign represent true positions of trackable object, small dot in graph represent trackable object estimation results over time and the bigger circle is a centroid product of the small dot cluster
Figure 4.10: Round 1 and 2, (+) sign represent true positions of trackable object, small dot in graph represent trackable object estimation results over time and the bigger circle is a centroid product of the small dot cluster
 Figure 4.11: Round 3 and 4, (+) sign represent true positions of trackable object, small dot in graph represent trackable object estimation results over time and the bigger circle is a centroid product of the small dot cluster
Figure 4.11: Round 3 and 4, (+) sign represent true positions of trackable object, small dot in graph represent trackable object estimation results over time and the bigger circle is a centroid product of the small dot cluster
As explained in the beginning of this section, we predict a smartphone position at different angles in different true positions. For instance, we predict a smartphone at true position A and the same in true position B, then we use the results to calculate and predict the position of trackable object in C etc.
The results from the experiments are presented in the following eight different graphs. Each graph has two centroids of two predicted smartphone positions of four different directions with cross (X) sign, smartphones have true positions with plus (+) sign, small dots are generated by our trilateration method from combination of two predicted smartphone on different direction and a big circle that represent the centroid of all small dots for trackable object.
Before we start with looking into the eight graphs, we present a graph as an example 4.12 and explain the signs:
+ sign: True position
X sign: Centroid of Smartphone predicted position
O sign: Centroid of trackable object predicted position o sign: Predicted positions of trackable object
A position top left
B position bottom left
C position bottom right
D position top right
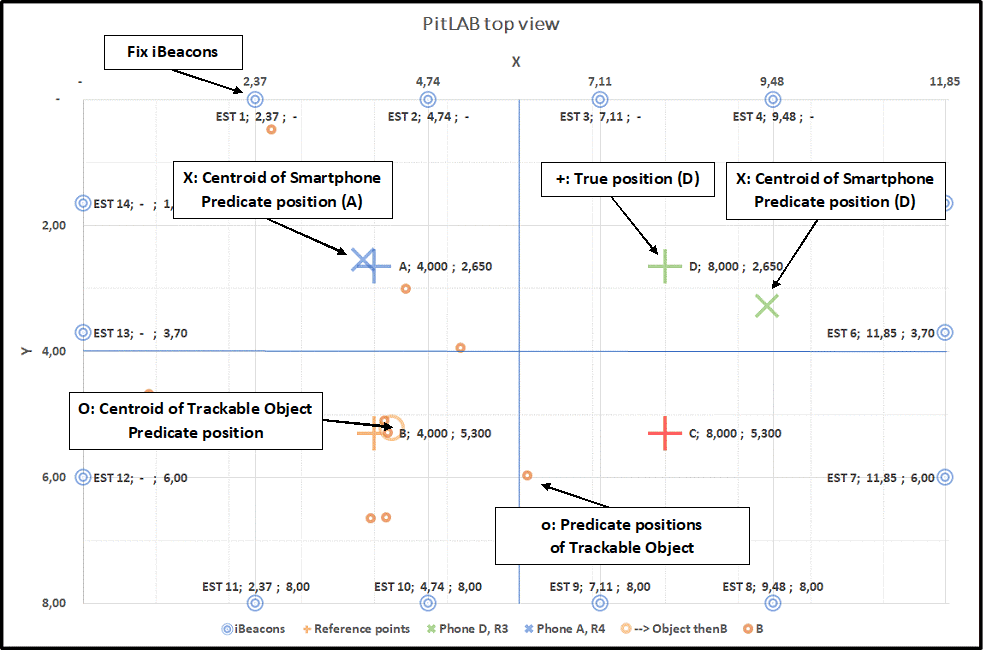 Figure 4.12: Graph: This is a sample graph with explanation of different signs we use in the upcoming graphs.
Figure 4.12: Graph: This is a sample graph with explanation of different signs we use in the upcoming graphs.
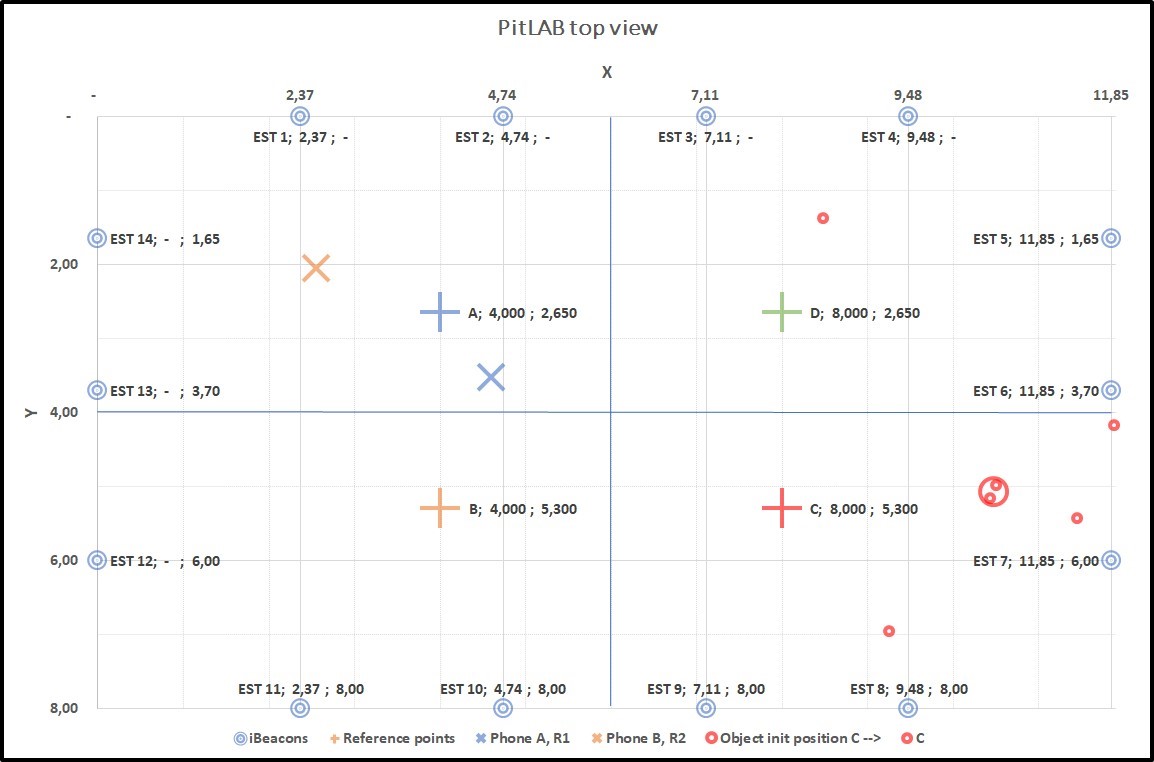 Figure 4.13: Graph1: Collecting data from two true positions A(+) and B(+). A(X) and B(X) smartphone predicted position, B(X) is far away from B(+), result of this predict position of trackable object centroid C(O) with true position of C(+)
Figure 4.13: Graph1: Collecting data from two true positions A(+) and B(+). A(X) and B(X) smartphone predicted position, B(X) is far away from B(+), result of this predict position of trackable object centroid C(O) with true position of C(+)
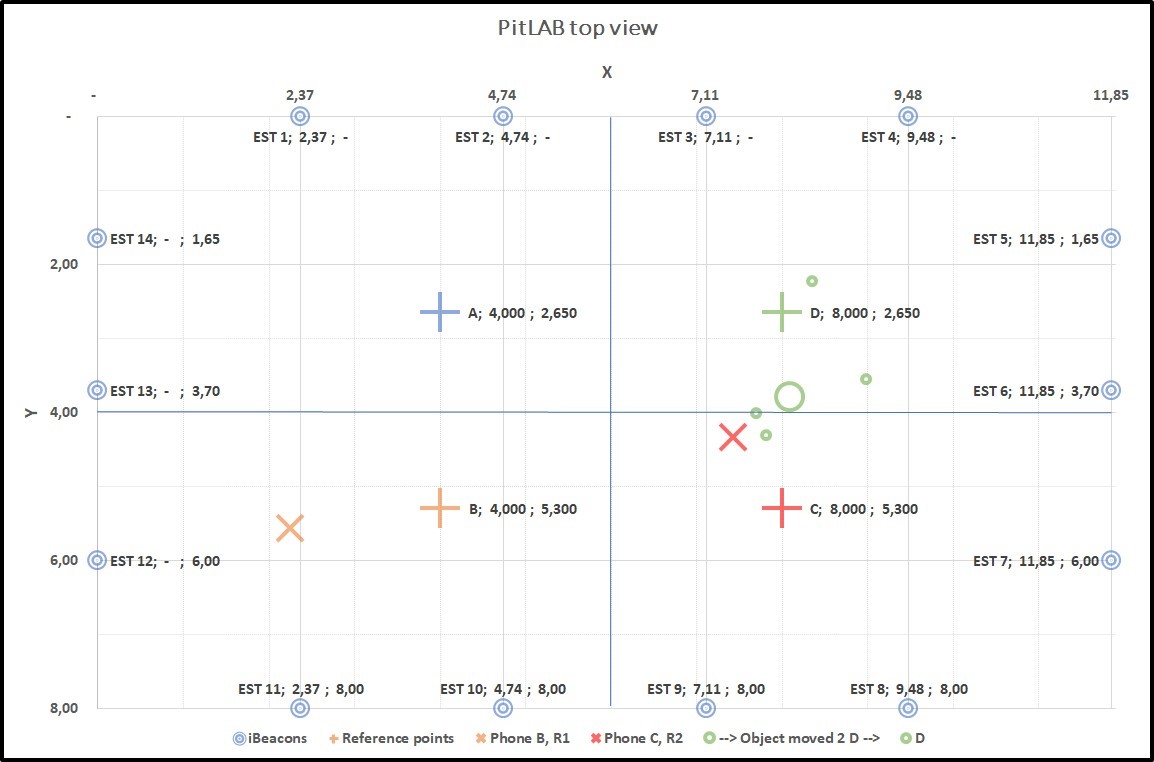 Figure 4.14: Graph2: Collecting data from two true positions B(+) and C(+). B(X) and C(X) smartphone predicted position, result of this predicted position of trackable object centroid D(O) with true position of D(+)
Figure 4.14: Graph2: Collecting data from two true positions B(+) and C(+). B(X) and C(X) smartphone predicted position, result of this predicted position of trackable object centroid D(O) with true position of D(+)
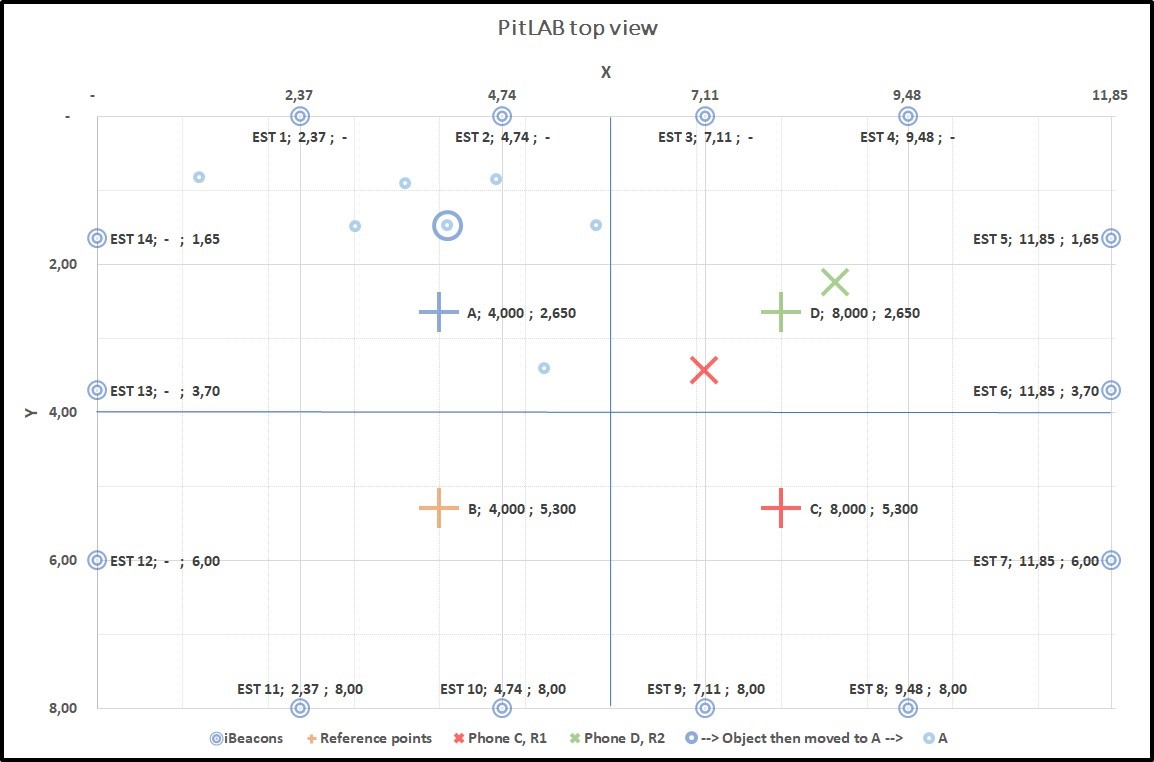 Figure 4.15: Graph3: Collecting data from two true position C(+) and D(+). C(X) and D(X) smartphone predicted position, C(X) is far away from C(+), result of this predicted position of trackable object centroid A(O) with true position of A(+)
Figure 4.15: Graph3: Collecting data from two true position C(+) and D(+). C(X) and D(X) smartphone predicted position, C(X) is far away from C(+), result of this predicted position of trackable object centroid A(O) with true position of A(+)
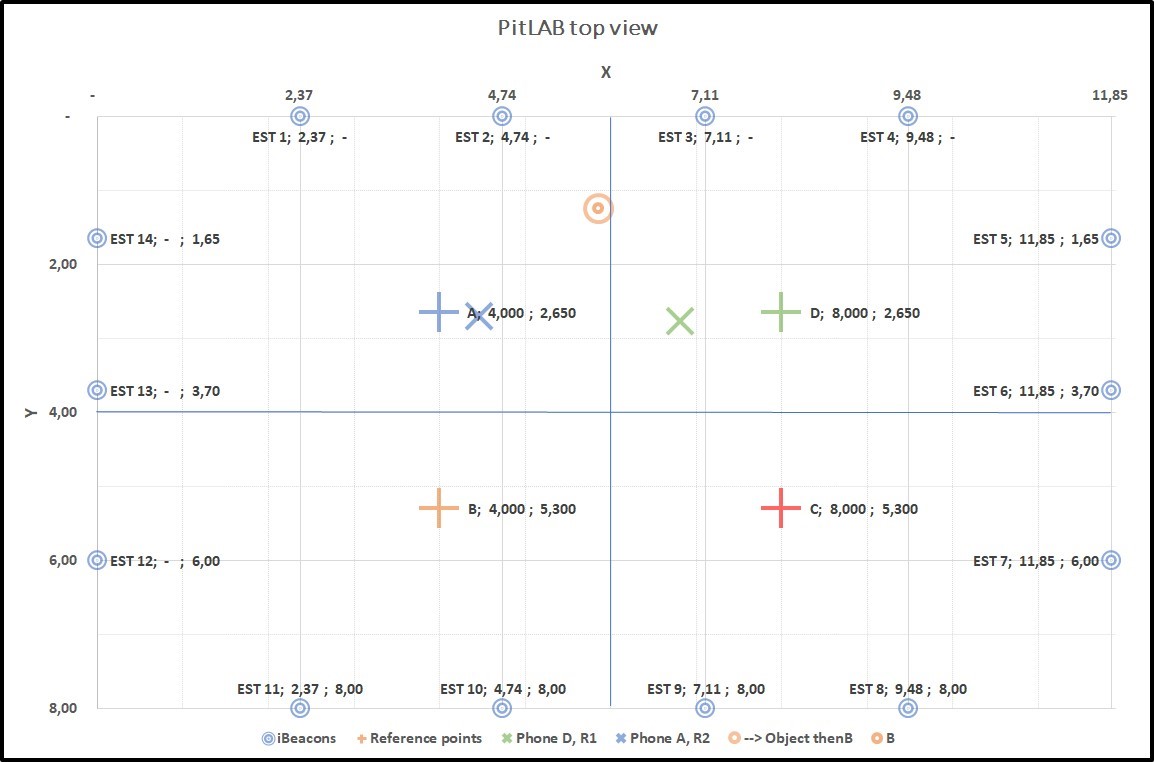 Figure 4.16: Graph4: Collecting data from two true positions D(+) and A(+). D(X) and A(X) smartphone predicted position, result of this predicted position of trackable object centroid A(O) with true position of B(+), Our algorithm was only able to predict one position
Figure 4.16: Graph4: Collecting data from two true positions D(+) and A(+). D(X) and A(X) smartphone predicted position, result of this predicted position of trackable object centroid A(O) with true position of B(+), Our algorithm was only able to predict one position
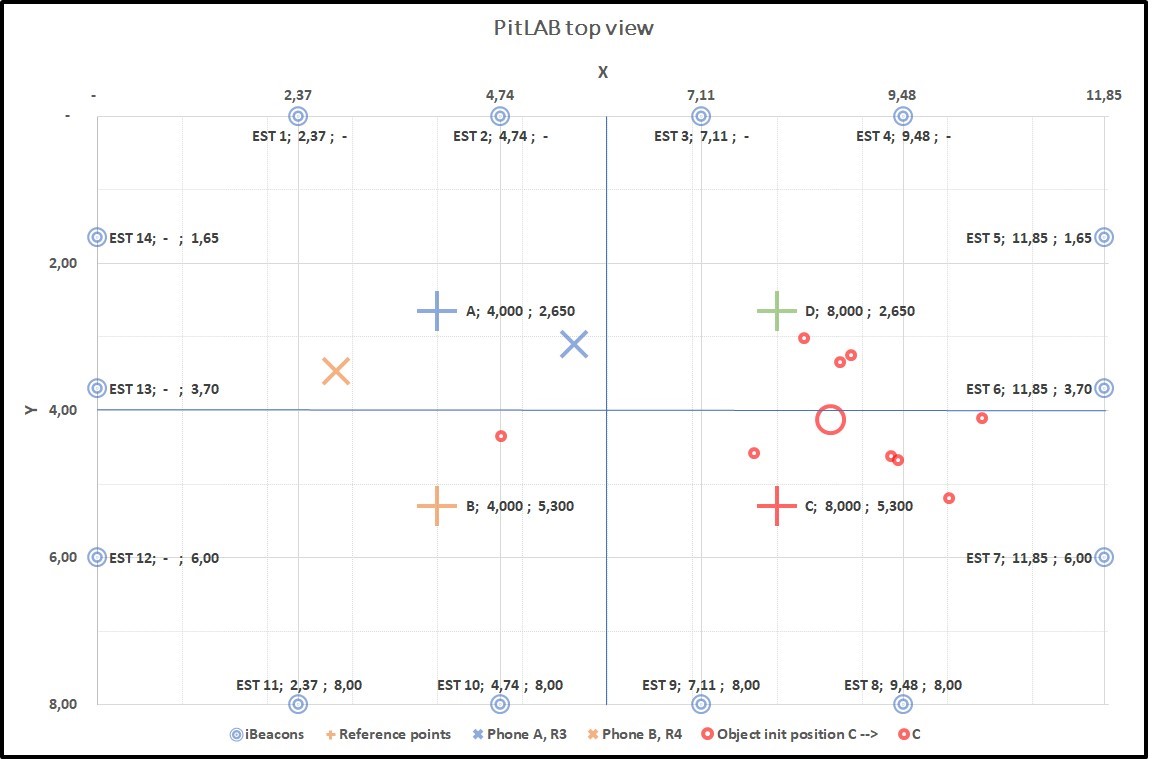 Figure 4.17: Graph5: Collecting data from two true positions A(+) and B(+). A(X) and B(X) smartphone predicted position, B(X) is far a way from B(+), result of this predicted position of trackable object centroid C(O) with true position of C(+)
Figure 4.17: Graph5: Collecting data from two true positions A(+) and B(+). A(X) and B(X) smartphone predicted position, B(X) is far a way from B(+), result of this predicted position of trackable object centroid C(O) with true position of C(+)
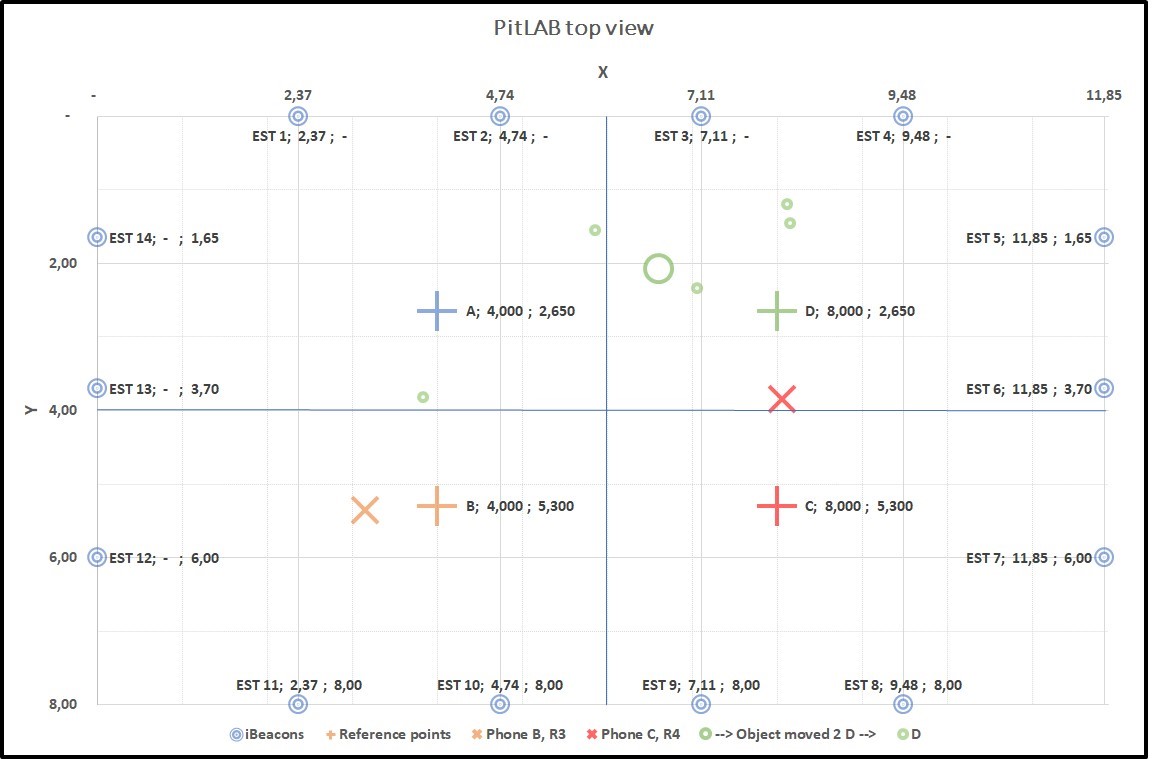 Figure 4.18: Graph6: Collecting data from two true positions B(+) and C(+). B(X) and C(X) smartphone predicted position, C(X) is far away from C(+), result of this predicted position of trackable object centroid D(O) with true position of D(+)
Figure 4.18: Graph6: Collecting data from two true positions B(+) and C(+). B(X) and C(X) smartphone predicted position, C(X) is far away from C(+), result of this predicted position of trackable object centroid D(O) with true position of D(+)
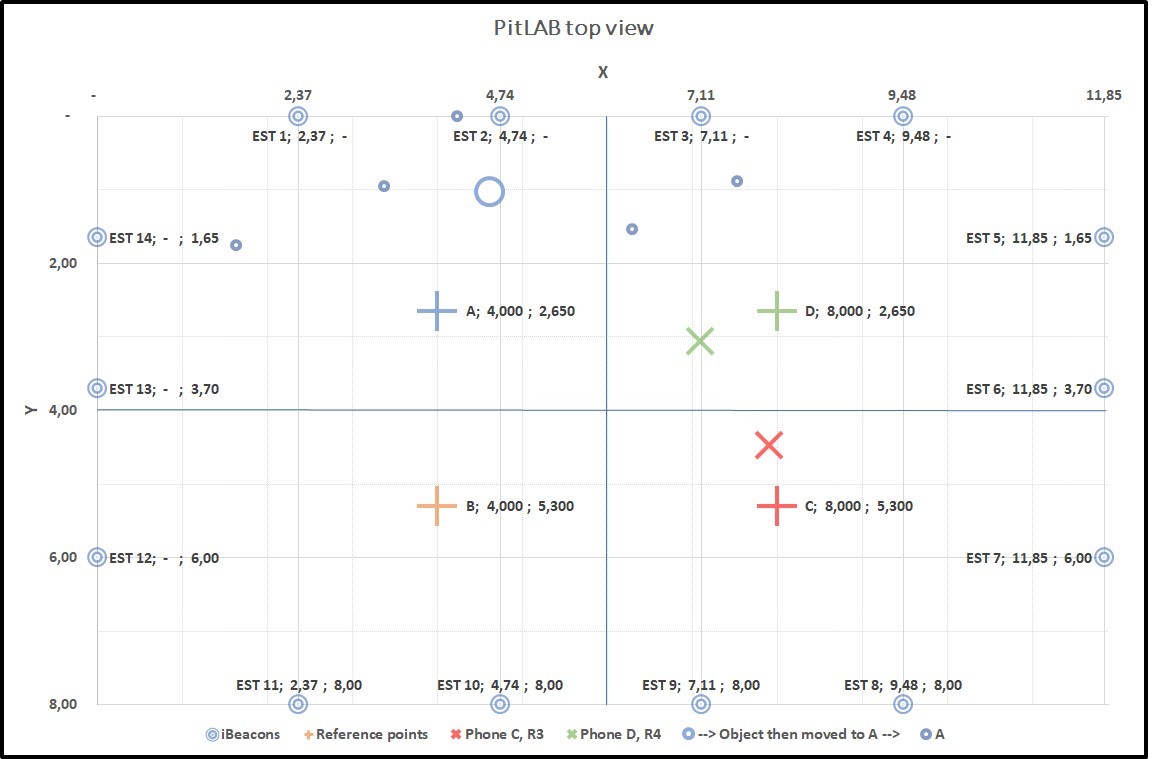 Figure 4.19: Graph7: Collecting data from two true positions C(+) and D(+). C(X) and D(X) smartphone predicted position, result of this predicted position of trackable object centroid A(O) with true position of A(+)
Figure 4.19: Graph7: Collecting data from two true positions C(+) and D(+). C(X) and D(X) smartphone predicted position, result of this predicted position of trackable object centroid A(O) with true position of A(+)
 Figure 4.20: Graph8: Collecting data from two true positions D(+) and A(+). D(X) and A(X) smartphone predicted position, result of this predicted position of trackable object centroid B(O) with true position of B(+)
Figure 4.20: Graph8: Collecting data from two true positions D(+) and A(+). D(X) and A(X) smartphone predicted position, result of this predicted position of trackable object centroid B(O) with true position of B(+)
Since we have an average error level of 2.04 meter 4.4 with standard deviation of 0.28 meter 4.4, so if we want to visualize trackable object position on a map it would be much better to present it in a more human friendly and readable way.
In our map, we have four true positions. If we split the room horizontally and vertically in half, this would give use four regions, where each true position belongs to its respective region as described earlier.
The same convention is used as before AR, BR, CR and DR. AR stays for A Region, B Region, etc. If we take the trackable object position result from the previous graphs, then we can present the trackable object position in its region and its movement over time. As we can see in the first graph the trackable object has moved over time from C to D, D to A and A to B is its final move.
In the first graph, we see trackable object move over time on the respective path, expect A to B. If we look back in Graph4 4.16, we can see we have only one dot, where we normally should have at least more than one dot as shown in graph 4.21. Our system has failed to calculate the results of the particular place. The reason for this can vary, but one reason might be that the particular time there could be affecting heavily with noise.
If we take the next graph, the trackable object follows the path as expected as shown in graph 4.22.
Depending on the room size and the error level, we assume it is possible to split the room in more regions to get smoother results. That said, we conclude that continues data collecting from more phones over time will improve accuracy of the prediction of position results.
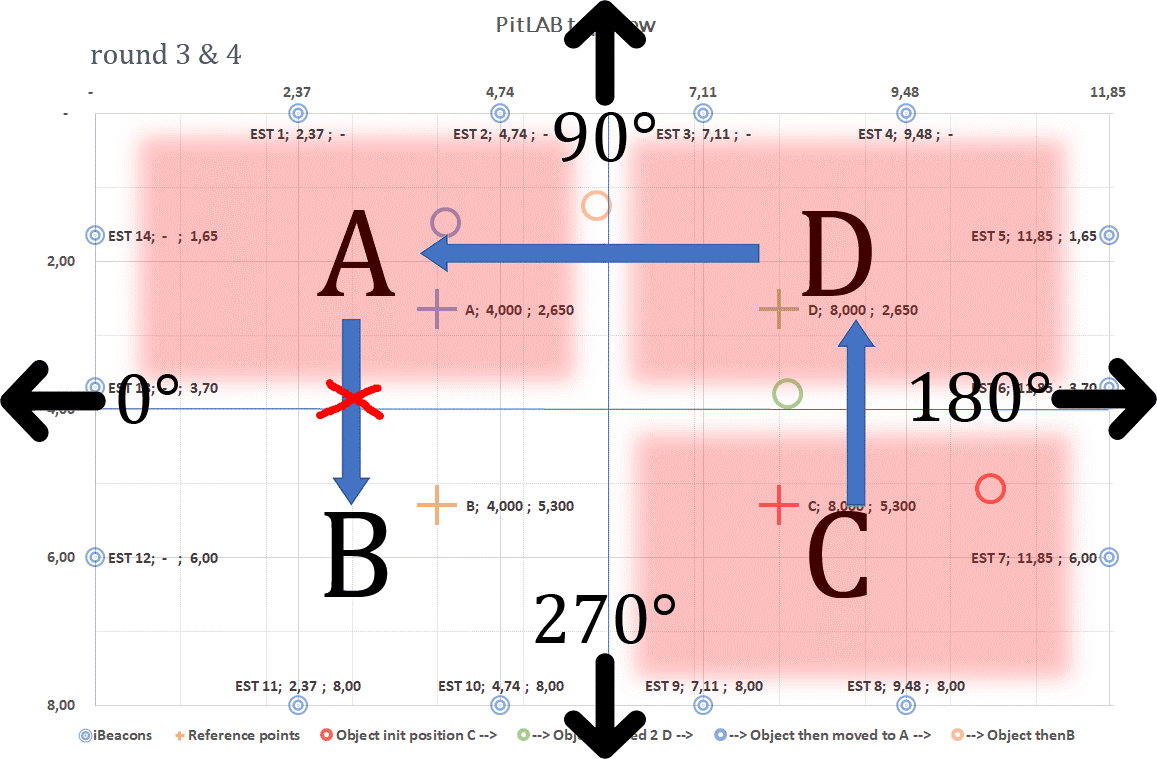 Figure 4.21: In this graph we illustrate trackable object location in regions and its movement from place to place over time. This is a result of combination of Round 1 and 2. As we can see the trackable object suppose to move to B region, since our system fails to calculate the results. This means trackable objects stop at A region
Figure 4.21: In this graph we illustrate trackable object location in regions and its movement from place to place over time. This is a result of combination of Round 1 and 2. As we can see the trackable object suppose to move to B region, since our system fails to calculate the results. This means trackable objects stop at A region
 Figure 4.22: In this graph we illustrate trackable object location in regions and its movement from place to place over time. This is a result of combination of Round 3 and 4.
Figure 4.22: In this graph we illustrate trackable object location in regions and its movement from place to place over time. This is a result of combination of Round 3 and 4.
4.4 Error level
We have in chapter 2 under section RSSI measurement 2.2.2 talked about iBeacon and smartphone challenges and in same chapter talked about RSSI distance calculation 2.8 which shows the measuring errors over distance of our iBeacon. If we take all that into consideration and look at our results we discover an error margin in our results as well.
We have made two graphs to illustrate the error level of our system. The first graph demonstrates error level of a smartphone. We present the results of each Round and for each true position point in table. Then we calculate the hypotenuse of X and Y to get the distance of the error and present that in Cumulative distribution function (CDF) graph 4.24. We can see that our overall results have distribution of error at different levels but interesting enough that almost 75% of the results have error level below 1.5 meter with average of 1.33 meter error and standard deviation of 0.13 meter.
However, in the Cumulative distribution function (CDF) graph 4.26, for trackable object, we can see the error average has raised to 2.04 meter with standard deviation of 0.28 meter. The interesting aspect of this graph is that 75% of the results are below 2 meter.
If we compare the error of trackable object to our smartphone, we see the trackable object error level is higher than the one from smartphones. This is due t nature results, hence the trackable object get its position result from smartphone positions which already have error margin.
We calculate the hypotenuse with the following formula: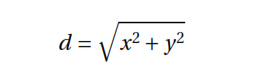 d = error distance from true position.
d = error distance from true position.
 Figure 4.23: Smartphone distance error of each axis x and y for each true position and for each round, with average value of each round.
Figure 4.23: Smartphone distance error of each axis x and y for each true position and for each round, with average value of each round.
 Figure 4.24: CDF graph for smartphone distance error of hypotenuse results from x and y from previous table for each round
Figure 4.24: CDF graph for smartphone distance error of hypotenuse results from x and y from previous table for each round
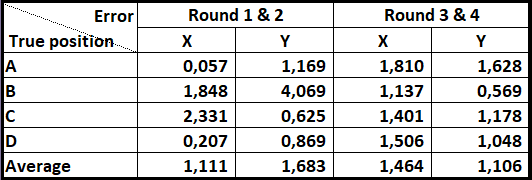 Figure 4.25: Trackable object distance error of each axis x and y for each true position and for each combined rounds, with average value of each round.
Figure 4.25: Trackable object distance error of each axis x and y for each true position and for each combined rounds, with average value of each round.
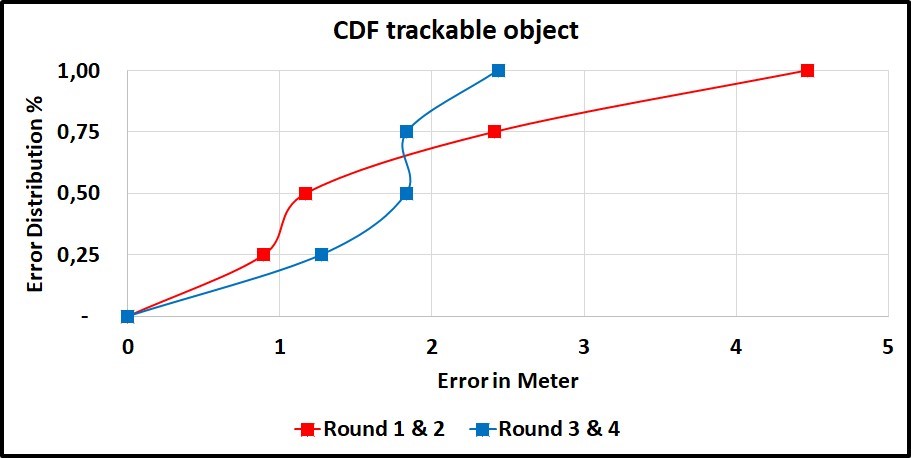 Figure 4.26: CDF graph for trackable object error of hypotenuse results from x and y from previous table for each combined rounds.
Figure 4.26: CDF graph for trackable object error of hypotenuse results from x and y from previous table for each combined rounds.
4.5 Conclusion of this chapter
We conclude that BLE signals in iBeacon is hard to control. Even Estimote (the company that produces iBeacon, which we use in our experiment) mention the issue of precision on their website 1. It is around 20-30%. This said, we cannot control the behaviour of BLE nature. In addition, we have learned that we need to predict a high number of smartphone position before we can predict our trackable object. However, by developing and improving algorithms, we will be able to get some useful results.


